Trapping Rain Water II

Given an m x n matrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.

Note:
Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.

Example:

Given the following 3x6 height map:
[
  [1,4,3,1,3,2],
  [3,2,1,3,2,4],
  [2,3,3,2,3,1]
]

Return 4.

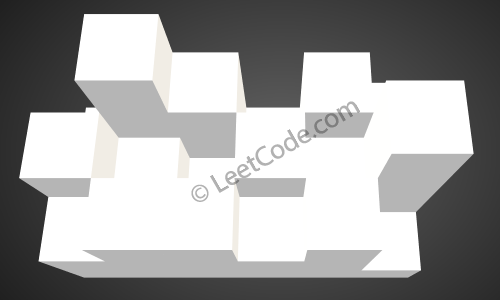
The above image represents the elevation map [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] before the rain.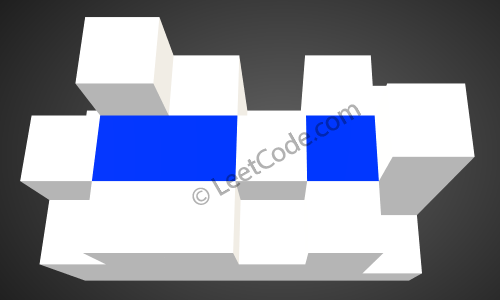

After the rain, water are trapped between the blocks. The total volume of water trapped is 4.

When it turns to 3D , it becomes a little bit more difficult.

We know that the highest amount of water the container can hold depends on the lowest height in the surroundings. Thus we can use a min-heap, first put all surrounding cells in it. Then each time poll out the cell with the lowest height, find if it has unvisited even lower neighbors, and add water to it (calculate sum). Now once we pour the water in it, the height of the neighbor cell should have the same height as the original cell (if it is not higher, in which case we cannot put water in it), and thus later we can track how much water it can help its neighbors hold, so we need to put the maximum height of the current cell and neighbors cell into the queue. 

There was one concern I had, which can be explained using the following graph:

Consider I have an elevation map like this (looking from top down). Now the current cell I poll out is cell 1, its neighbor cell 2 has a lower height. Cell 3 is an unvisited neighbor of cell 2, which has a lower height than cell 1 but higher than cell 2. My question was why do we add height difference between cell 1 and 2 without checking cell 3? 

To explain this, we need to involve another boundary cell 4. There are two cases, first, cell 4 has already been visited, second, it's not. For the first case, if it is already visited, we are sure it has lower height than cell 1, and we know its neighbor cell 3 has lower height then cell 1, which should also be visited, so it doesn't satisfy our condition. For the second case, cell 4 should be higher than cell 1. The water the container can hold in this column is determined by cell 1, even if cell 3 has lower height than cell 1, it will be filled by water with the same height as cell 1 later because cell 4 has a higher height. So in the end both cell 2 and cell 3 will be filled with water. 

public int trapRainWater(int[][] heightMap) {
        int m = heightMap.length;
        if (m == 0) {
            return 0;
        }
        int n = heightMap[0].length;
        if (n == 0) {
            return 0;
        }
        PriorityQueue<Cell> pq = new PriorityQueue<>();
        boolean[][] visited = new boolean[m][n];
        for (int i = 0; i < m; i++) {
            pq.add(new Cell(i, 0, heightMap[i][0]));
            visited[i][0] = true;
            pq.add(new Cell(i, n - 1, heightMap[i][n - 1]));
            visited[i][n - 1] = true;
        }
        
        for (int j = 1; j < n - 1; j++) {
            pq.add(new Cell(0, j, heightMap[0][j]));
            visited[0][j] = true;
            pq.add(new Cell(m - 1, j, heightMap[m - 1][j]));
            visited[m - 1][j] = true;
        }
        
        int[] dirX = {0, 0, -1, 1};
        int[] dirY = {-1, 1, 0, 0};
        int sum = 0;
        while (!pq.isEmpty()) {
            Cell curr = pq.poll();
            for (int i = 0; i < 4; i++) {
                int nx = curr.x + dirX[i];
                int ny = curr.y + dirY[i];
                if (nx >= 0 && nx < m && ny >= 0 && ny < n && !visited[nx][ny]) {
                    sum += Math.max(0, curr.h - heightMap[nx][ny]);
                    pq.add(new Cell(nx, ny, Math.max(heightMap[nx][ny], curr.h)));
                    visited[nx][ny] = true;
                }
            }
        }
        return sum;
    }
    
    private class Cell implements Comparable<Cell> {
        int x, y, h;
        public Cell(int x, int y, int h) {
            this.x = x;
            this.y = y;
            this.h = h;
        }
        
        public int compareTo(Cell other) {
            return h - other.h;
        }
    }