Check if a string has all unique characters
public boolean isUnique(String s) {
if (s == null)
throw new NullPointerException("Null string!");
if (s.length() == 0)
return true;
int check = 0;
for (int i = 0; i < s.length(); i++) {
int val = Character.getNumericValue(s.charAt(i));
if ((check & (1 << val)) > 0)
return false;
check |= (1 << val);
}
return true;
}
Insert bits
You are given two 32-bit numbers, N and M, and two bit positions, i and j.Write a method to set all bits between i and j in N equal to M (e.g., M becomes a substring of N located at i and starting at j).
Set all positions after j to zero
Set all positions after i back to 1
get the mask where all bits between i to j is cleared
put m into n from ith position
public int insertBitnumber(int m, int n, int posi, int posj) {
//32 bit of 1s == -1;
int max = ~0;
/* e.g., posj = 3
* 1 << posj = 1000
* (1 << posj) - 1 = 111
* max - that will leave all bits after j = 0;
*/
int left = max - ((1 << posj) - 1);
int right = (1 << posi) - 1;
//this operation will leave all positions between posi and posj equals zero
int mask = left | right;
//mask & n will clear all bits between i and j in n
// then we put m in those positions
return (mask & n) | (m << posi);
}
Decimal To Binary
Given a (decimal - e.g.3.72) number that is passed in as a string, print the binary representation.If the number can not be represented accurately in binary, print “ERROR” .
Given an binary integer, we know that 1001 = 1 * 2^ 3 + 0 * 2 ^ 2 + 0 * 2 ^ 1 + 1 * 2^0 = 9. So if we keep doing mod operation and divide the number by 2, we can get the binary representation of the integer.
Analogously, 0.101 = 1 * (1/2)^1 + 0 * (1/2)^2 + 1 * (1/2)^3 = 0.625. Thus if we multiply the number by 2, we get 1 * (1/2)^0 + 0 * (1/2)^1 + 1 * (1/2)^2 = 1.25
(10) = 1.01
(2). So if the result is greater than 1, we know that there should be 1 follows "." in the decimal part. We can do the same operation for every digit.
public class DecimalToBinary {
public String decimalToBinary (String s) {
if (s == null)
throw new NullPointerException("Null string");
int intPart = Integer.parseInt(s.substring(0, s.indexOf('.')));
double deciPart = Double.parseDouble(s.substring(s.indexOf('.')));
String rst = "";
while (intPart > 0) {
rst = String.valueOf(intPart % 2) + rst;
intPart >>= 1;
}
rst += ".";
String decim = "";
while (deciPart > 0) {
if (decim.length() > 32) {
return "Error";
}
if (deciPart == 1) {
decim += "1";
break;
}
double d = deciPart * 2;
if (d >= 1) {
decim += "1";
deciPart = d - 1;
}
else {
decim += "0";
deciPart = d;
}
}
return rst + decim;
}
}
Next Largest and Smallest number that has the same number of 1 bits
Given an integer, print the next smallest and next largest number that have the same number of 1 bits in their binary representation.
Ok, this is interesting. So basically, given a binary number, 11100110, if we want to find the next largest one that has the same number of 1 bits, we first switch the first 0 to 1, which gives us 11101110, then we switch the next 1 after that 0 to 0, and results in 11101010. Since we want the next largest, we would want to shift all the 1s after that to the most right side, and the result is: 11101001, yep, here is the solution.
The next smallest number is similar. Reversely, we switch the first 1 to 0 and the next 0 to 1. Using another example 110011 would result in 101011, and shifts, and the answer is: 101110.
public class NextBitNumber {
private int setBit(int n, int index, boolean toOne) {
int rst;
if (toOne)
rst = n | (1 << index);
else {
int mask = ~ (1 << index);
rst = n & mask;
}
return rst;
}
private boolean getBit(int n, int index) {
return (n & (1 << index)) > 0;
}
public int nextLargest(int n) {
if (n <= 0)
return -1;
int index = 0;
int countOnes = 0;
while (!getBit(n, index))
index++;
while(getBit(n, index)) {
index++;
countOnes++;
}
n = setBit(n, index, true);
index--;
n = setBit(n, index, false);
countOnes--;
index--;
for (int i = index; i > index - countOnes; i--)
n = setBit(n, i, false);
for (int i = 0; i < countOnes; i++)
n = setBit(n, i, true);
return n;
}
public int nextSmallest(int n) {
if (n <= 0)
return -1;
int index = 0;
int countZeros = 0;
while (getBit(n, index)) {
index++;
}
while (!getBit(n, index)) {
index++;
countZeros++;
}
n = setBit(n, index, false);
index--;
n = setBit(n, index, true);
index--;
countZeros--;
for (int i = index; i > index - countZeros; i--)
n = setBit(n, i, true);
for (int i = 0; i < countZeros; i++)
n = setBit(n, i, false);
return n;
}
}
What does (n & (n - 1)) == 0 used for?
Check if n == 0 or power of 2!
For example, 100 and 11;
Bits needed to convert a number to another number
Write a function to determine the number of bits required to convert integer A to integer B.
Input: 31, 14
Output: 2
Count the number of different bits in a number by using XOR.
public class BitsNeededToConvert {
public int bitsNeeded(int a, int b) {
if (a == b)
return 0;
int count = 0;
for (int c = a ^ b; c >= 0; c = c>> 1) {
count += c & 1;
}
return count;
}
}
Something about Hexadecimal
In Unix shells, and C programming language:
prefix
0x for numeric constants represented in hex. e.g., 0x5A3 (1443
10).
Character and string constants may express characters codes in hexadecimal with the prefix
\x followed by two hex digits: \x1B (Esc control character)
Unicode standard:
A character value is represented with
U+ followed by the hex value, e.g., U+20AC
(euro sign)
Convert hexadecimal to binary
Swap odd and even bits in a number
Write a program to swap odd and even bits in an integer with as few instructions as possible (e.g., bit 0 and bit 1 are swapped, bit 2 and bit 3 are swapped, etc).
shift all odd bits left for 1 position and shift all even bits right for 1 position
public class SwapBits {
public int swapBits (int n) {
//0xaaaaaaaa = 10101010...10
// 0x55555555 = 1010101...01
return (n & 0xaaaaaaaa) >> 1 | (n & 0x55555555) << 1;
}
}


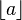 denotes the
denotes the 
